(Kls X) Blog Fisika Pak Ahmad: IMPULS dan MOMENTUM

1. Impuls

impuls dan momentum

Anda telah mengetahui bahwa yang menyebabkan suatu benda diam menjadi bergerak adalah gaya. Misalnya: bola golf yang mula-mula diam akan bergerak ketika gaya pukulan stik golf anda bekerja pada bola golf tersebut (perhatikan gambar di atas). Gaya pukulan stik golf anda pada bola golf termasuk gaya kontak yang bekerja hanya dalam waktu yang singkat. Gaya seperti ini disebut gaya impulsif. Perkalian antara gaya tersebut dengan selang waktu gaya itu bekerja pada benda disebut Impuls.

Impuls secara matematis, dituliskan sebagai berikut:

$I=F.\Delta t$
dengan
I = impuls (Ns)
F = gaya impulsif (N)
$\Delta t$ = perubahan waktu (t2-t1)

Impuls adalah hasil kali antara besaran vektor gaya F dengan besaran skalar selang waktu 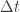$\Delta t$ , sehingga impuls termasuk besaran vektor. Arah impuls I searah dengan arah gaya impulsif F.

Jika gaya impulsif F, yang berubah terhadap selang waktu 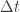$\Delta t$ , dapat anda gambarkan grafik F-t nya, maka luas arsir dalam selang waktu 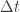$\Delta t$ , dimana 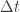$\Delta t$ = t2 – t1, sama dengan luas arsir di bawah grafik F-t, dengan batas nilai dari t1 sampai dengan t2 (gambar berikut).

Impuls = Luas daerah di bawah grafik F-t

Contoh

1. Sebuah bola biliard dipukul dengan gaya 20 N dalam selang waktu 0,5 sekon. Tentukan Impuls yang bekerja pada bola biliard tersebut!
Diketahui:
F = 20 N
$\Delta t$ = 0,5 sekon
Ditanyakan: I = ……?
Jawab:
I = F. $\Delta t$ = 20 N × 0,5 s = 10 Ns
Jadi besarnya impuls yang bekerja pada bola biliard tersebut adalah 10 Ns.

2. Perhatikan gambar berikut!
grafik-impuls

Tentukanlah besar impulsnya!
Penyelesaian:
Gaya 10 N bekerja selama selang waktu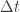 $\Delta t$ = 6 – 4 = 2 s. Impuls yang dilakukan gaya tersebut adalah 20 Ns.
Luas daerah yang diarsir di bawah grafik F terhadap t sama dengan (10 N) × (2 s) = 20 Ns.

Dari persamaan impuls dapat disimpulkan bahwa gaya dan selang waktu berbanding terbalik. Perhatikan tabel berikut:

Besarnya impuls yang dibentuk adalah sebesar 200 Ns, namun besar gaya dan selang waktu gaya tersebut bekerja pada benda bervariasi. Dari Tabel di atas tersebut, dapat dilihat bahwa jika waktu terjadinya tumbukan semakin besar (lama), gaya yang bekerja pada benda akan semakin kecil. Oleh karena itu, dapat disimpulkan bahwa waktu kontak antara gaya dan benda sangat mempengaruhi besar gaya yang bekerja pada benda saat terjadi tumbukan.

Aplikasi Impuls dalam Keseharian dan Teknologi

Prinsip memperlama selang waktu kontak bekerjanya impuls agar gaya impulsif yang dihasilkan menjadi lebih kecil, banyak diaplikasikan dalam peristiwa keseharian.

1. Mengapa di bagian dalam helm selalu ada gabus/sponnya?

Ketika terjadi benturan, misalkan impuls yang dihasilkan oleh helm tanpa spon dan helm dengan spon adalah sama. Tetapi selang waktu kontak antara helm dengan spon lebih lama dibandingkan dengan helm tanpa spon. Hal ini akan menghasilkan gaya impulsif yang lebih kecil. Gaya impulsif yang lebih kecil akan memberikan rasa sakit yang lebih kecil. Sehingga helm dengan spon akan mengurangi rasa sakit jika terjadi benturan.
2. Mengapa pertandingan atau latihan judo selalu diadakan di atas matras?

judo-jepang-beladiri-paling-mematikan-didunia-infoinfo-unik

Ketika pejudo dibanting di atas matras atau lantai, impuls yang dialaminya sama. Tetapi karena selang waktu kontak antara punggung pejudo dan matras berlangsung lebih lama daripada antara punggung pejudo dan lantai, maka gaya impulsif yang dikerjakan matras pada punggung lebih kecil daripada gaya impulsif yang dikerjakan lantai pada punggung. Sebagai akibatnya, pejudo yang dibanting di lantai tidak dapat menahan rasa sakit akibat bantingan yang dialaminya.

3. Mengapa karateka selalu menarik kepalan tangannya secara cepat sewaktu memukul lawannya?

Ini dimaksudkan agar selang waktu kontak antara kepalan tangan karateka dan badan lawan yang dipukulnya berlangsung sesingkat mungkin sehingga lawannya menderita gaya impulsif yang lebih besar.

4. Mengapa ketika kita membeli barang elektronik baru seperti TV, di dalam kardus TV tersebut pasti ada gabus yang membungkus TV tersebut?

Ini dimaksudkan agar ketika kardus TV itu terjatuh atau terbentur sesuatu, waktu kontak sampai mengenai TV menjadi lebih lama. Dengan waktu kontak yang lebih lama, maka gaya impulsif yang dihasilkan akan lebih kecil. Gaya impulsif yang kecil, akan memungkinkan kerusakan TV bisa dihindari.

2. Momentum

Perhatikan gambar di atas. Jika kedua kendaraan tersebut bergerak dengan kecepatan sama, manakah yang lebih sukar anda hentikan: kendaraan yang bermassa besar atau kecil? Jika dua kendaraan bermassa sama (misalnya truck dengan truck, atau mobil dengan mobil) bergerak mendekati anda, manakah yang lebih sukar anda hentikan: kendaraan dengan kecepatan tinggi atau rendah?
Momentum didefinisikan sebagai ukuran kesukaran untuk memberhentikan suatu benda. Dari jawaban anda terhadap dua pernyataan di atas, momentum dirumuskan sebagai hasil kali massa dan kecepatan.

P = m . v

dengan
P = momentum (kg m/s)
m = massa (kg)
v = kecepatan (m/s)

Momentum diperoleh dari hasil kali besaran skalar massa dan besaran vektor kecepatan, sehingga momentum termasuk besaran vektor. Arah momentum searah dengan arah kecepatan. Untuk momentum satu dimensi, arah momentum cukup ditampilkan dengan tanda positif atau negatif.

Contoh

Sebuah mobil bermassa 1000 kg bergerak dengan kecepatan 36 km/jam. Berapakah momentum mobil tersebut?
Diketahui:
m = 1000 kg
v = 36 km/jam = 36.1000/3600 m/s = 10 m/s
Ditanyakan: P = …?
Jawab:

P = m . v = 1000 x 10 = 10.000

Jadi besarnya momentum mobil tersebut adalah 10.000 kg.m/s.

3. Hukum Kekekalan Momentum

Suatu tumbukan selalu melibatkan sedikitnya dua benda. Misalnya benda itu adalah bola biliar A dan B (Gambar di atas). Sesaat sebelum tumbukan, bola A bergerak mendatar ke kanan dengan momentum mAvA dan bola B bergerak mendatar ke kiri dengan momentum mBvB. Momentum sistem partikel sebelum tumbukan tentu saja sama dengan jumlah momentum bola A dan bola B sebelum tumbukan.

$P_{A}+P_{B}=m_{A}v_{A}+m_{B}v_{B}$

Momentum sistem partikel sesudah tumbukan tentu saja sama dengan jumlah momentum bola A dan bola B sesudah tumbukan.

$P^{'}_{A}+P^{'}_{B}=m_{A}v^{'}_{A}+m_{B}v^{'}_{B}$

Hukum Kekekalan Momentum Linear
Dalam peristiwa tumbukan, momentum total sistem sesaat sebelum tumbukan sama dengan momentum total sistem sesaat sesudah tumbukan, asalkan tidak ada gaya luar yang bekerja pada sitem.

Formulasi hukum kekekalan momentum linear di atas dinyatakan oleh:

$P_{A}+P_{B}=P^{'}_{A}+P^{'}_{B}$
$m_{A}v_{A}+m_{B}v_{B}=m_{A}v^{'}_{A}+m_{B}v^{'}_{B}$

Contoh

Sebuah bola bilyard 1 dengan massa 30 g dan kecepatan 0,5 m/s bergerak ke kanan mengenai bola bilyard 2 dengan massa 30 g yang diam di bidang datar tanpa gesekan. Jika kecepatan bola bilyard 1 setelah tumbukan 1 m/s ke arah kiri, maka hitunglah kecepatan bola bilyard 2 setelah tumbukan!
Diketahui:
m1 = 30 g = 0,03 kg
v1 = 0,5 m/s
m2 = 30 g = 0,03 kg
v2 = 0
v1’ = -1 m/s (tanda (-) menyatakan gerak ke kiri)
Ditanyakan: v2’ = ….?
Jawab:
Menurut Hukum Kekekalan Momentum Linear

$P_{A}+P_{B}=P^{'}_{A}+P^{'}_{B}$
$m_{A}v_{A}+m_{B}v_{B}=m_{A}v^{'}_{A}+m_{B}v^{'}_{B}$
$0.03 x 0,5 + 0,03 x 0=0,03 x (-1)+0,03v^{'}_{B}$
$0.015 + 0=-0,03+0,03v^{'}_{B}$
$0.015 + 0,03=0,03v^{'}_{B}$
$0.045=0,03v^{'}_{B}$
$v^{'}_{B}=\frac{0.045}{0,03}=1,5m/s$
Karena nilainya positif, jadi bola billiard 2 bergerak ke kanan.

4. Hubungan Impuls dan Momentum

Perhatikan Gambar di atas. Sebuah bola datang ke arah pemain bola dengan kecepatan awal vaw sesaat sebelum ditendang. Sesaat sesudah ditendang (impuls bekerja), kecepatan akhir bola vak. Sesuai dengan hukum II Newton, maka:

F=m.a
Karena percepatan rata-rata
$a=\frac{\Delta v}{\Delta t}=\frac{v_{ak}-v_{aw}}{\Delta t}$
maka
$F=m\left ( \frac{v_{ak}-v_{aw}}{\Delta t} \right )$
$F.\Delta t=mv_{ak}-mv_{aw}$
$F.\Delta t=P_{ak}-P_{aw}$
$I=\Delta P$

Persamaan tersebut dapat kita nyatakan dengan kalimat berikut dan dikenal sebagai Teorema Impuls-Momentum:
Impuls yang dikerjakan pada suatu benda sama dengan perubahan momentum yang dialami benda itu, yaitu beda antara momentum akhir dengan momentum awalnya.

Contoh

Sebuah bola bermassa 0,15 kg pada permainan softball dilempar mendatar ke kanan dengan kelajuan 20 m/s. Setelah dipukul, bola bergerak ke kiri dengan kelajuan 20 m/s.
a. Berapakah impuls yang diberikan oleh kayu pemukul pada bola?
b. Jika kayu pemukul dan bola bersentuhan selama 0,80 ms, berapakah gaya rata-rata yang diberikan kayu pemukul pada bola?
c. Hitung percepatan rata-rata bola selama bersentuhan dengan kayu pemukul!

Penyelesaian:
Massa bola = 0,15 kg
Kecepatan awal v1 = +20 m/s (arah ke kanan)
Kecepatan akhir v2 = -20 m/s (arah kekiri)
a. Impuls yang diberikan kayu pemukul pada bola sama dengan perubahan momentum bola.
$I=\Delta P$
$I=P_{ak}-P_{aw}$
$I=mv_{ak}-mv_{aw}$
$I=0,15.(-20)-0,15.(+20)=-3-3=-6Ns$
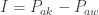
Tanda negatif menyatakan bahwa impuls berarah mendatar ke kiri
b. Selang waktu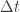 $\Delta t$ = 0,80 ms = 8 x 10-4 s
$I=F.\Delta t$
$F=\frac{I}{\Delta t}=\frac{-6}{8x10^{-4}}=-0,75x10^{4}=-7500N$
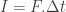
Gaya rata-rata kayu pemukul pada bola

F=7500N
c. Percepata rata-ratanya
$F=m.a$
$a=\frac{F}{m}=\frac{-7.500}{0,1}=-50.000m/s^{2}$
Tanda negatif menyatakan bahwa arah percepatan adalah mendatar ke kiri.

5. Hukum II Newton dalam Bentuk Momentum✅

6. Tumbukan

Dalam kehidupan ini, banyak kita jumpai peristiwa tumbukan. Tumbukan dapat terjadi pada saat benda yang bergerak mengenai benda lain yang sedang bergerak atau diam. Pembahasan akan dibatasi mengenai tumbukan sentral lurus, yaitu tumbukan antara dua benda yang arah kecepatannya berimpit dengan garis hubung kedua pusat massa benda. Berdasarkan sifat kelentingan atau elastisitas benda yang bertumbukan, tumbukan dapat dibedakan menjadi tiga jenis, yaitu tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali.

a. Tumbukan Lenting Sempurna

Dua buah benda dikatakan mengalami tumbukan lenting sempurna jika pada tumbukan itu tidak terjadi kehilangan energi kinetik. Jadi, energi kinetik total kedua benda sebelum dan sesudah tumbukan adalah tetap. Pada tumbukan lenting sempurna berlaku hukum kekekalan momentum dan hukum kekekalan energi kinetik. Dua buah benda memiliki massa masing-masing m1 dan m2 bergerak saling mendekati dengan kecepatan sebesar v1 dan v2 sepanjang lintasan yang lurus. Setelah keduanya bertumbukan masing-masing bergerak dengan kecepatan sebesar v’1 dan v’2 dengan arah saling berlawanan.

Berdasarkan hukum kekekalan momentum dapat ditulis sebagai berikut.

Sedangkan berdasarkan hukum kekekalan energi kinetik, diperoleh persamaan sebagai berikut.

Jika persamaan di atas saling disubtitusikan, maka diperoleh persamaan sebagai berikut.

Ruas sebelah kanan menunjukkan kelajuan relatif setelah tumbukan dan ruas kiri adalah kelajuan relatif sebelum tumbukan. Kelajuan relatif setelah tumbukan sama dengan kelajuan relatif sebelum tumbukan tapi arahnya berlawanan.

Harga 1 pada persamaan di atas menyatakan keofisien restitusi untuk tumbukan lenting sempurna. Secara umum persamaan tersebut dapat ditulis sebagai berikut.

Dalam hal ini, e adalah koefisien restitusi. Persamaan di atas berlaku untuk semua jenis tumbukan.

e = 1, untuk tumbukan lenting sempurna.
e = 0, untuk tumbukan tidak lenting sama sekali.
0 < e < 1, untuk tumbukan lenting sebagian.

b. Tumbukan Lenting Sebagaian

Pada tumbukan lenting sebagian, beberapa energi kinetik akan diubah menjadi energi bentuk lain seperti panas, bunyi, dan sebagainya. Akibatnya, energi kinetik sebelum tumbukan lebih besar daripada energi kinetik sesudah tumbukan. Pada tumbukan lenting sebagian berlaku Hukum Kekekalan Momentum, tetapi tidak berlaku Hukum Kekekalan Energi Kinetik. Pada tumbukan lenting sebagian, koefisien restitusi (e) nilainya adalah 0 < e < 1. Besarnya koefisien restitusi benda dapat ditentukan dengan persamaan:

dengan
e = koefisien restitusi
h1 = ketinggian mula-mula
h2 = ketinggian setelah memantul

c. Tumbukan Tidak Lenting Sama Sekali

Tumbukan tidak lenting sama sekali merupakan peristiwa tumbukan dua benda yang memiliki ciri setelah tumbukan kedua benda bersatu (perhatikan gambar di atas). Keadaan ini dapat digunakan bahasa lain, setelah bertumbukan; benda bersama-sama, benda bersarang dan benda bergabung. Kata-kata itu masih banyak lagi yang lain yang terpenting bahwa setelah bertumbukan benda menjadi satu. Jika tumbukannya seperti gambar di atas maka koefisien restitusinya akan nol, e = 0. Pada tumbukan ini berlaku hukum kekekalan momentum, tetapi energi kinetiknya tidak kekal. Pada tumbukan tidak lenting sama sekali, sesudah tumbukan kedua benda bersatu, sehingga kecepatan kedua benda sesudah tumbukan besarnya sama, yaitu v1′ = v2′ = v’.
Sumber

Di bawah ini dapat dijadikan pengetahuan tambahan tentang terbentuknya koefisien restitusi (e).

Berdasarkan sifat kelentingan benda, tumbukan dibedakan menjadi tiga jenis, yaitu tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali. Dengan menggunakan Hukum Kekekalan Momentum dan Hukum Kekekalan Energi, kita dapat menentukan peristiwa yang terjadi setelah tumbukan.

1. Tumbukan Lenting Sempurna

Apabila tidak ada energi yang hilang selama tumbukan dan jumlah energi kinetik kedua benda sebelum dan sesudah tumbukan sama, maka tumbukan itu disebut tumbukan lenting sempurna. Pada tumbukan lenting sempurna berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik. Misalnya, dua buah benda massanya masing-masing m₁ dan m₂ bergerak dengan kecepatan v₁ dan v₂ dengan arah berlawanan seperti pada gambar berikut.

Tumbukan lenting sempurna antara dua benda:

(a) sebelum tumbukan, (b) saat tumbukan, (c) setelah tumbukan.

Kedua benda bertumbukan lenting sempurna, sehingga setelah tumbukan kecepatan kedua benda menjadi v₁' dan v₂' . Berdasarkan Hukum Kekekalan Momentum, dituliskan:

m₁ v₁ + m₂ v₂ = m₁ v₁' + m₂v₂'

m₁ v₁ – m₁v₁' = m₂ v₂' – m₂v₂

m₁(v₁ – v₁' ) = m₂(v₂' – v₂)

(i)

Dari Hukum Kekekalan Energi Kinetik diperoleh:

ii)

Jika persamaan (ii) dibagi dengan persamaan (i) diperoleh:

v₁ + v₁' = v₂' + v₂

v₁' – v₂' = v₂– v₁

v₁' – v₂' = -(v₁ – v₂ )

(2)

Persamaan (2) dapat dituliskan:

(3)

Bilangan pada persamaan (3) disebut koefisien restitusi (e), yang merupakan negatif perbandingan kecepatan relatif kedua benda sebelum tumbukan. Persamaan (3) dapat dinyatakan:

(4)

Dengan demikian, pada tumbukan lenting sempurna koefisien restitusi (e) = 1.

contoh soal tumbukan lenting sempurna

2. Tumbukan Lenting Sebagian

Pada tumbukan lenting sebagian berlaku Hukum Kekekalan Momentum, tetapi tidak berlaku Hukum Kekekalan Energi Kinetik.

ΣEk > ΣEk ' , maka:

Ek₁+ Ek₂ > Ek₁' + Ek₂'

v₂– v₁> v₁' – v₂'

Sehingga persamaan (3) dapat dituliskan:

(5)

Dengan demikian, dapat disimpulkan pada tumbukan lenting sebagian, koefisien restitusi (e) adalah:

0 < e < 1.

Untuk menentukan koefisien restitusi benda yang bertumbukan, perhatikan contoh berikut ini. Perhatikan gamba berikut!

Tumbukan lenting sebagian antara bola dengan lantai.

Sebuah bola elastis jatuh bebas dari ketinggian h₁ dari lantai, maka akan terjadi tumbukan antara bola dengan lantai sehingga bola memantul setinggi h₂. Berdasarkan persamaan pada gerak jatuh bebas, kecepatan benda sesaat sebelum tumbukan adalah:

Gerak bola sesaat setelah terjadi tumbukan dapat diidentifikasikan dengan gerak jatuh bebas, sehingga:

(arah ke atas negatif)

Karena lantai diam, maka kecepatan lantai sebelum dan sesudah tumbukan adalah nol, v₂ = v₂ ' = 0, sehingga besarnya koefisien restitusi adalah:

contoh soal tumbukan lenting sebagian

3. Tumbukan tidak Lenting Sama Sekali

Pada tumbukan tidak lenting sama sekali, sesudah tumbukan kedua benda bersatu, sehingga kecepatan kedua benda sesudah tumbukan besarnya sama, yaitu v₁' = v₂' = v'. Berdasarkan Hukum Kekekalan Momentum maka:

m₁ v₁ + m₂ v₂ = m₁ v₁' + m₂v₂'

m₁v₁ + m₂ v₂ = (m₁ + m₂ ) v'

Karena v₁' = v₂' , maka v₁' – v₂' = 0, sehingga koefisien restitusi (e) adalah:

Jadi, pada tumbukan tidak lenting sama sekali besarnya koefisien restitusi adalah nol (e =0).

Sumber